fig1
RIDUZIONE, IN PROPORZIONE, DI UNA FIGURA GEOMETRICA
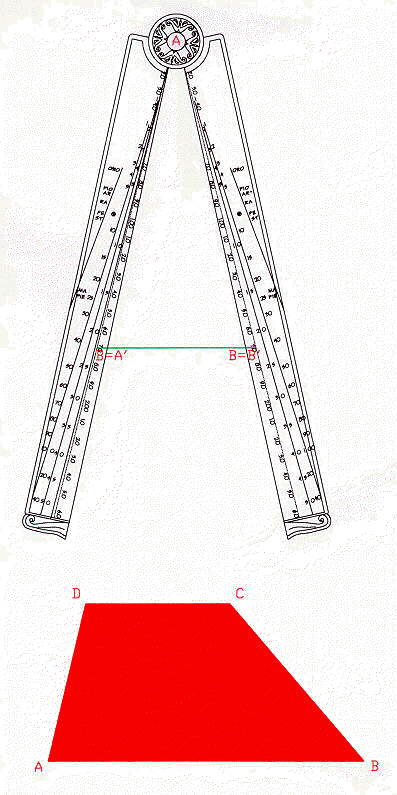
Vogliamo ridurre di 1/2 le dimensioni del trapezio ABCD.
Riportiamo con un compasso a doppia punta la misura del lato AB sulla scala aritmetica, riprodotta sul braccio destro e sinistro del compasso, partendo dal suo fulcro, origine della scala. Avendo scelto come rapporto di similitudine 1/2, calcoliamo la misura del lato corrispondente
A’B’ = 1/2 . AB
Riportiamo la misura A’B’ trasversalmente rispetto al compasso aprendo il compasso in modo che l’estremo B’ coincida con la misura riportata precedentemente sul secondo braccio del compasso.
fig.1

fig1
Senza variare l’apertura del compasso, troveremo le misure degli altri lati corrispondenti nel seguente modo: riportiamo sul primo braccio la misura, presa col compasso a due punte, del lato BC e troveremo quella del corrispondente B’C’ tracciando la parallela per C ad A’B’. L’intersezione di tale parallela col secondo braccio del compasso segnerà l’estremo C’ (fig.2)
Si esegue lo stesso procedimento per trovare le misure di C’D’ e di D’A’.
|
figura iniziale |
figura ridotta |
||
|
lato |
misura (cm) |
lato |
misura (cm) |
| AB | 16 | A’B’ | 8 |
| BC | 10,5 | B’C’ | 5,3 |
| CD | 7,3 | C'D' | 3,7 |
| AD | 8,3 | A'D' | 4,2 |
Trovati tutti i lati del poligono simile, resta il problema di riportare correttamente gli angoli. Nel nostro esempio, per riportare correttamente l’angolo DAB , troveremo seguendo il procedimento appena esposto, la misura della diagonale B’D’;
|
figura iniziale |
figura ridotta |
||
| diag. | misura (cm) | diag. | misura (cm) |
| BD | 16,2 | B’D’ | 8,1 |
| AC | 12,2 | A’C’ | 6,1 |
Con l’aiuto di un compasso, riporteremo la sua misura partendo da B’, ripetiamo l’operazione per il lato A’D’: il punto di intersezione sarà D’ e si individuerà il triangolo A’B’C’.
Per ingrandire il quadrilatero ABCD, dovremo riportare sulla scala aritmetica, riprodotta sul primo braccio del compasso, la misura di A’B’ e trasversalmente quella di AB e poi procedere allo stesso modo.
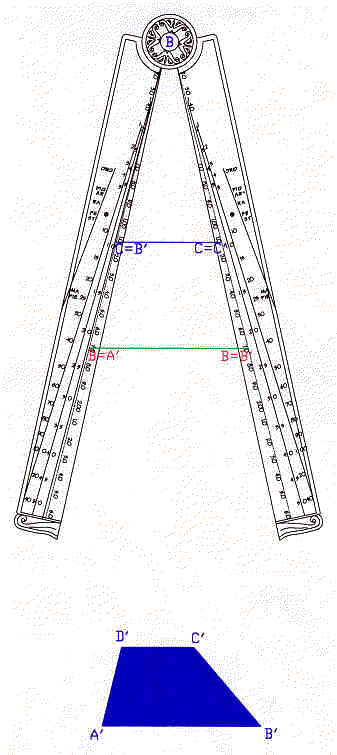
fig.2