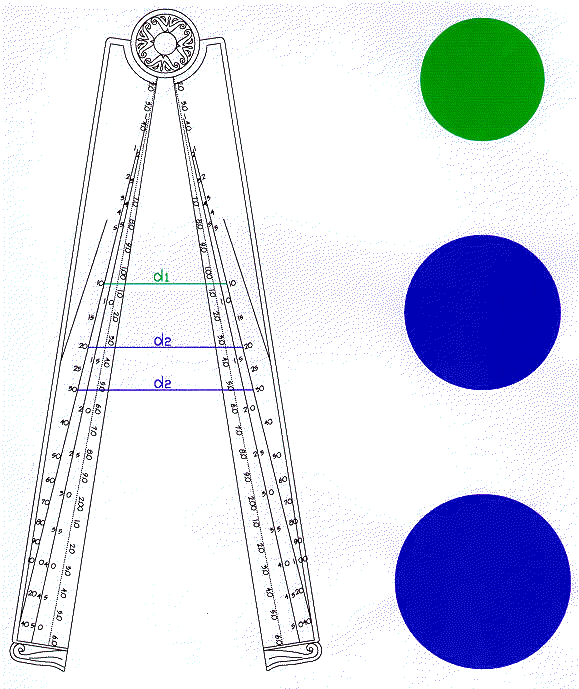
DETERMINAZIONE DI UN SOLIDO DI VOLUME
n- VOLTE QUELLO DI UN CAMPIONE
Vogliamo trovare una sfera di volume doppio di quello di una sfera campione.
V2 = 2.V1
Con il compasso
a due punte prendiamo la misura del diametro
d1 = a1
della sfera campione e lo
riportiamo trasversalmente tra e punti
x1 = 10 della
scala
stereometrica, aprendo
opportunamente il compasso.
Bloccando l’apertura
così ottenuta,
prendiamo trasversalmente la
misura tra i punti corrispondenti alle tacche
20. Tale misura sarà il
diametro d2
della sfera cercata;
segue
Il rapporto tra
i diametri e quindi tra i raggi è
;
quello tra i volumi è 2.
Se vogliamo
trovare la misura del diametro d2 di una sfera di
volume triplo
rispetto a quello campione, una volta
bloccata l’apertura del
compasso, considereremo la
distanza tra i numeri
x2 = 30
quale misura del diametro cercato.
Infatti
Il rapporto tra
i diametri e quindi tra i raggi è
; quello tra i volumi è
3.
|
sfera iniziale |
sfera di volume doppio |
||
|
d1 (cm) |
V1 (cm3) |
d2 (cm) |
V2 (cm3) |
|
5 |
65,449 |
6,3 |
130,924 |
|
sfera iniziale |
sfera di volume triplo |
||
|
d1 (cm) |
V1 (cm3) |
d2 (cm) |
V2 (cm3) |
|
5 |
65,449 |
7,1 |
187,401 |