Dato il triangolo rettangolo ABC, il cateto AB contiene infiniti punti, dato che il punto non ha dimensioni e quindi è privo di lunghezza.
Sia D il punto medio di AC e per esso tracciamo il segmento DE parallelo ad AB.
I triangoli ABC e CDE sono simili; segue che anche i lati corrispondenti sono in proporzione ed in particolare, vista la scelta del punto D su AB, anche DE è la metà di AB

Secondo Simplicio è immediato, concludere che il segmento AB contenga un numero di punti maggiore di DE, e più precisamente affermare che, pur contenendo tanto AB quanto DE infiniti punti, AB ne contenga il doppio di DE (fig.1).
Ecco il paradosso:
il segmento AB contiene il doppio dei punti di DE, ma al tempo stesso contiene lo stesso numero di punti di DE.
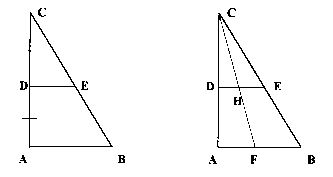
fig.1
fig.2
Oggi diremo che i punti di AB e di DE sono in corrispondenza biunivoca, e cioè sono in uguale numero.
Prendiamo a caso un punto F su AB e congiungiamolo con C: il segmento FC taglia DE in H. Ad ogni punto F di AB corrisponde un solo punto H di DE. Possiamo anche procedere iversamente, prendendo un punto qualsiasi H su DE e congiungendolo con C; ad ogni punto H di DE corrisponderà un solo punto F di AB (fig.2).
E poichè DE è una parte di AB, vediamo che quando gli elementi che compongono un insieme sono infiniti, il tutto non è maggiore della parte, ma è uguale ad una sua parte.
| Nella matematica moderna, questo paradosso viene utilizzato per dare una definizione di INSIEME INFINITO. | Galileo ha compreso pienamente la caratteristica di quello che noi chiamiamo "un insieme di infiniti elementi", e delle contradizioni cui conducono i confronti qualitativi tra detti insiemi infiniti, potendo coesistere le relazioni di uguaglianza e di diseguaglianza. |
Galileo ha compreso pienamente la caratteristica di quello che noi oggi chiamiamo "un insieme di infiniti elementi", e delle contraddizioni cui conducono i confronti qualitativi tra detti insiemi infiniti, potendo coesistere le relazioni di uguaglianza e di diseguaglianza.