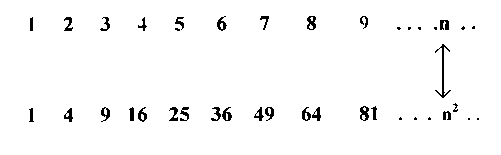
3° PARADOSSO
Per illustrare la questione, Galileo ricorre all'aritmetica e precisamente alla serie dei numeri naturali ed alla serie dei loro quadrati:
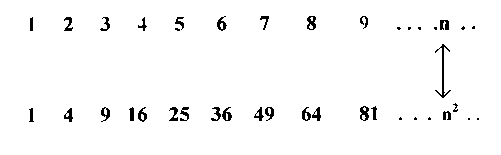
Entrambe le
serie contengono infiniti numeri.
Nella serie dei numeri naturali, solo alcuni sono dei quadrati perfetti, quindi,
prosegue Salviati
"se dirò che i numeri tutti, comprendendo i quadrati e i non quadrati, esser più che i quadrati soli, dirò una proposizione verissima".
D'altra parte, interrogatosi su quanti siano i numeri quadrati, Galileo afferma che sono tanti quante sono le loro radici e ogni radice ha un suo quadrato, ogni quadrato non può avere più di una radice e ogni radice ha un solo quadrato. Galileo riesce a mettere in "corrispondenza biunivoca" l' insieme dei naturali (radici) con l'insieme dei loro quadrati.
Inoltre i numeri quadrati entro il 100 sono 10 cioè la decima parte di 100.
1 4 9 16 25 36 49 64 81 100 ...
I numeri quadrati entro il 10.000 sono 100 cioè la centesima parte di 10.000.
I numeri quadrati entro 1.000.000 sono 1.000 cioè la millesima parte di 1.000.000.
I quadrati nella serie numerica diventano sempre più radi. La distanza tra il quadrato e il successivo va aumentando ogni volta di due unità e si ha quindi una rarefazione di quadrati sempre maggiore. Essi si ottengono, infatti, ciascuno dal precedente aggiungendo i successivi numeri dispari :
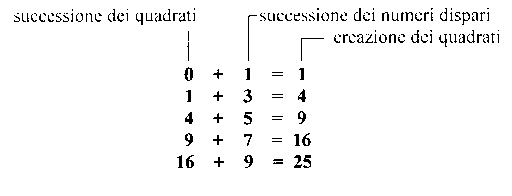
Galileo ricorda questa legge di formazione dei quadrati nella seconda giornata del Dialogo Sopra i due Massimi Sistemi, lì dove accenna alle leggi sulla caduta dei gravi.
Salviati conclude :
"Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti quadrati, infinite le loro radici, nè la moltitudine de' quadrati esser minore di quella di tutti i numeri, nè questa maggior di quella, ed in ultima conclusione, gli attributi di eguale e minore non aver luogo ne gl'infiniti, ma solo nelle quantità terminate".
Si è stabilito
il parallelismo tra il paradosso aritmetico dei numeri quadrati e quello
geometrico dei punti contenuti in linee di diversa lunghezza.