
riproduzione in ottone del
compasso
Esemplari di compasso galileiano,
costruiti con materiale povero dagli studenti, per verificare le operazioni
con le varie scale.
DESCRIZIONE DEL COMPASSO

riproduzione in ottone del
compasso
Esemplari di compasso galileiano,
costruiti con materiale povero dagli studenti, per verificare le operazioni
con le varie scale.
due regoli di ottone a sezione rettangolare (25 x 5 mm, lunghi 247 mm), fulcrati ad una estremità e arricchiti da incisioni e ornamenti; uno dei due bracci porta un foro che serve per fissare il filo a piombo quando si voglia usare il compasso come squadra per misurare l’inclinazione sulla scala delle linee inclinate.
un piedino o corsoio lavorato di circa 8 mm di lunghezza ("zanca", secondo la terminologia galileiana), che infilato in uno dei due regoli (o gambe) del compasso permette di mantenerlo verticale quando si usi come un quadrante o squadra appoggiato su di un piano o su di un cilindro; tale zanca permette anche di regolare la lunghezza della gamba in modo da far cadere un filo a piombo lungo una graduazione prescelta del quadrante.
un quadrante di ottone graduato che può essere avvitato con due galletti, pure di ottone, sui due bracci del compasso in modo che questi restino aperti a 90°;
Quando il compasso è chiuso esso forma una piastra unica sormontata da un rosone circolare di 30 mm di diametro, nel centro del quale, vi è un foro per fissarvi il filo di un piombino.

Il compasso presenta su ogni faccia delle coppie di scale, o linee, che analizziamo:
|
Il principio
sul quale si basa il
compasso galileiano, e tutti gli altri esemplari simili che sono apparsi nei
tempi seguenti, è
quello delle
proporzioni.
Aperto infatti il compasso ad un
angolo qualsiasi, avremo che le distanze trasversali
ai
e
ak stanno
tra loro come le distanze
yi e
yk.
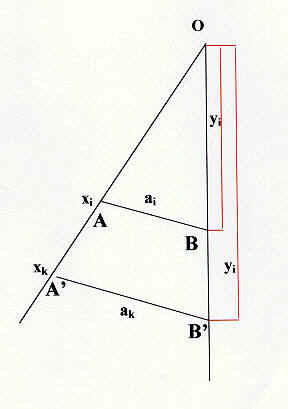
chiameremo xi e xk le letture dei punti generici i e k, cioè il numero che è inciso sulla scala a fianco dei numeri considerati.
Ricordiamo inoltre che, in tutti i problemi sulle scale qui esposti, per riportare le lunghezze dei segmenti, verrà usato un compasso a due punte